Music Segmentation¶

Detect structural changes in music using fastcpd.

Overview¶

Music segmentation identifies temporal boundaries between sections in a song (intro, verse, chorus, etc.). We use fastcpd’s RBF kernel to detect changes in the tempogram - a representation capturing tempo patterns over time.

Audio Example:

Dance of the Sugar Plum Fairy by Tchaikovsky (30 seconds)

Setup¶

pip install librosa matplotlib pyfastcpd

import librosa
from fastcpd.segmentation import rbf

Load and Process Audio¶

# Load 30 seconds of audio
signal, sr = librosa.load(librosa.ex("nutcracker"), duration=30)

# Compute tempogram (tempo representation)
hop_length = 256
oenv = librosa.onset.onset_strength(y=signal, sr=sr, hop_length=hop_length)
tempogram = librosa.feature.tempogram(onset_envelope=oenv, sr=sr, hop_length=hop_length)

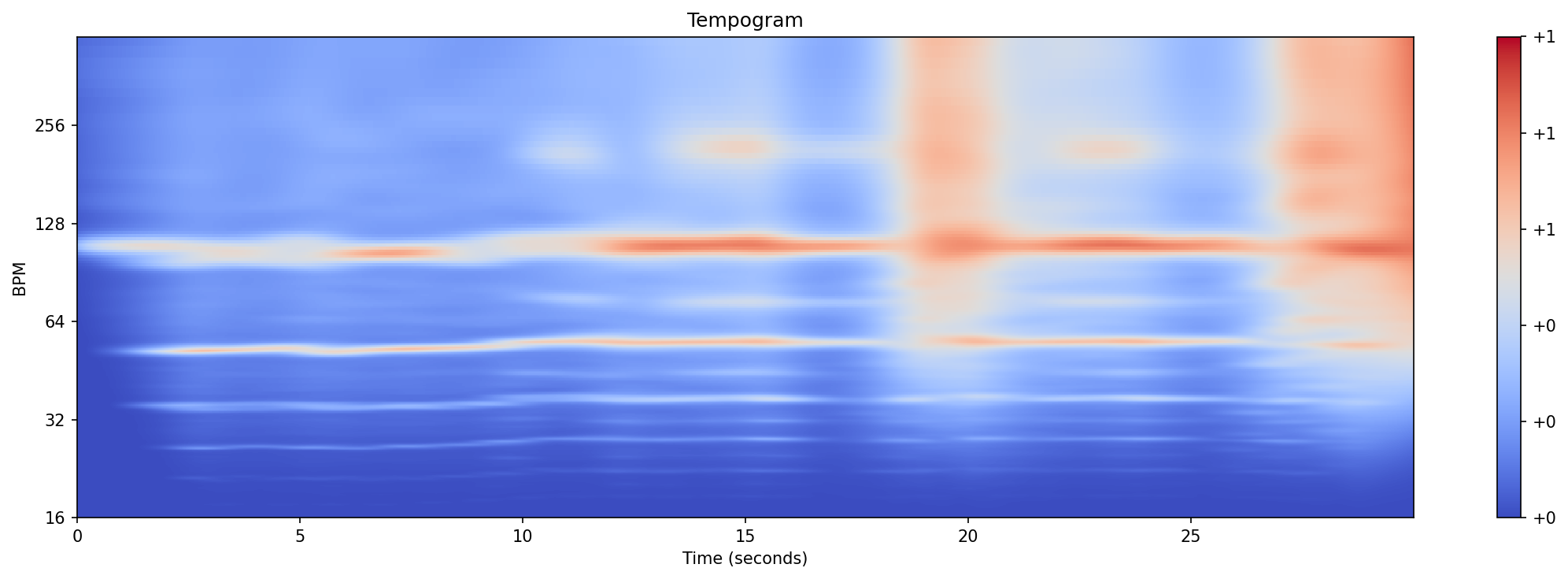
Detect Change Points¶

# Detect changes using RBF kernel (nonparametric method)
result = rbf(tempogram.T, beta=1.0)

# Convert to timestamps
times = librosa.frames_to_time(result.cp_set, sr=sr, hop_length=hop_length)
print(f"Detected {len(result.cp_set)} change points at: {times}")

Results¶

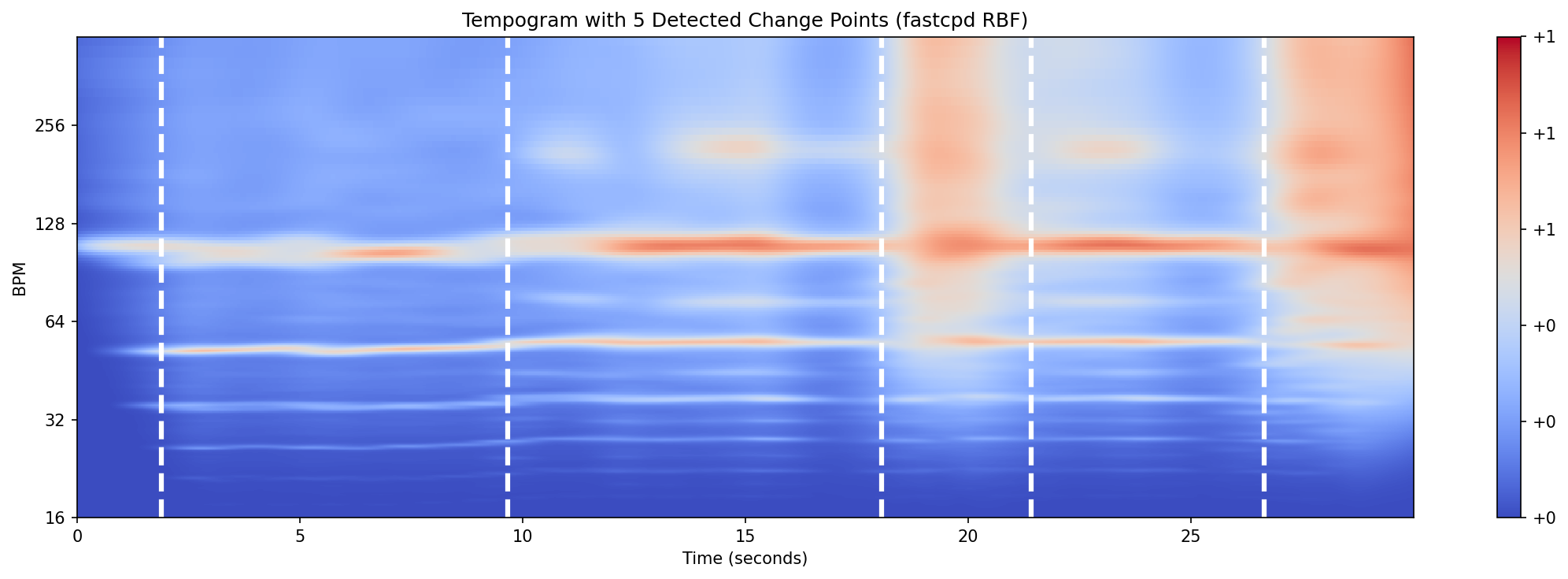
The algorithm detected 5 change points (white dashed lines) corresponding to major tempo transitions in the music.

Cost Function¶

For a segment from time \(s\) to time \(t\), the RBF kernel cost is:

\[c(s,t) = \sum_{i=s}^{t} k(y_i, y_i) - \frac{2}{t-s+1} \sum_{i,j=s}^{t} k(y_i, y_j)\]

where \(k(x, y) = \exp(-\gamma \|x - y\|^2)\) is the RBF kernel.

This measures the variance of data points in the embedded kernel space, with lower cost indicating more homogeneous segments.

Tuning Parameters¶

Adjust beta to control segmentation granularity:

rbf(data, beta=10)  # Conservative (fewer change points)
rbf(data, beta=1)   # Balanced (recommended)
rbf(data, beta=0.5) # Sensitive (more change points)

Complete Example¶

See examples/music_segmentation_example.py for a full runnable script with visualization.